Công thức Phạm vi là gì?
Công thức phạm vi đề cập đến công thức được sử dụng để tính toán sự khác biệt giữa giá trị lớn nhất và giá trị nhỏ nhất của phạm vi và theo công thức, giá trị nhỏ nhất được trừ khỏi giá trị lớn nhất để xác định phạm vi.
Phạm vi = giá trị lớn nhất - giá trị nhỏ nhất
Trong số các tập dữ liệu đã cho, cung cấp cho các nhà thống kê và nhà toán học hiểu rõ hơn về tập dữ liệu, nó đa dạng như thế nào. Đây là cách tiếp cận đơn giản nhất để tính phương sai trong thống kê.
Giải trình
Nó khá đơn giản và dễ sử dụng vì công thức cho biết Giá trị lớn nhất trừ giá trị nhỏ nhất của mẫu đã cho. Do đó, phương sai giữa giá trị lớn nhất và giá trị nhỏ nhất là Phạm vi, và mặc dù điều đó rất đơn giản để sử dụng và hiểu, nó yêu cầu phải diễn giải đúng.
Ví dụ: nếu có một trình phác thảo trong dữ liệu, phạm vi sẽ bị ảnh hưởng bởi phạm vi tương tự và sẽ nhận được kết quả sẽ dẫn đến trình bày sai. Lấy một ví dụ thực tế cho dữ liệu đã cho 2, 4, 7, 7, 100 thì phạm vi sẽ là 100 - 2, là 98, nhưng như người ta có thể thấy rằng phạm vi dữ liệu nằm dưới 10 nhưng xem xét và giải thích dữ liệu đó nằm trong 98 sẽ dẫn đến trình bày sai. Do đó, việc giải thích Phạm vi nên được tiến hành với sự cân nhắc thích đáng.
Ví dụ
Ví dụ 1
Hãy xem xét các tập dữ liệu sau 2,2,4,4, 4, 6,7,7,8, 8, 8, 9, 9, 9, 9, 9. Bạn được yêu cầu tính Phạm vi cho mẫu này.
Giải pháp:
- Giá trị lớn nhất = 9
- Giá trị nhỏ nhất = 2
Phạm vi = 9 - 2
Phạm vi = 7
Ví dụ số 2
Ông Stark, một nhà khoa học đang làm việc 10 năm với công ty mang tên Dream moon. Ông Arora, người giám sát của ông, đang tiến hành một thí nghiệm về sức khỏe con người và đã thu thập được một số dữ liệu mẫu về chiều cao của nam giới là 162, 158, 189, 144, 151, 150, 151, 178, 155, 160. Hiện ông đang bối rối và muốn biết có bao nhiêu dữ liệu đa dạng. Ông Stark, một nhà thống kê có kinh nghiệm, đã được người giám sát của ông, ông Arora, tiếp cận để loại bỏ sự nhầm lẫn của ông về sự biến đổi của công thức. Ông Arora được yêu cầu cung cấp câu trả lời cho người giám sát của mình; bạn được yêu cầu tính toán xem dữ liệu có đa dạng không?
Giải pháp:
Phạm vi = giá trị lớn nhất - giá trị nhỏ nhất
- Giá trị lớn nhất = 189
- Giá trị nhỏ nhất = 144
Phạm vi = 189 - 144
Phạm vi = 45
Dữ liệu hoặc mẫu được thu thập có độ biến thiên 45.
Ví dụ # 3
Ông Buffet, một nhà đầu tư nổi tiếng và được kính trọng trên khắp thế giới, hiện đang xem xét cổ phiếu thị trường Hoa Kỳ và đang trong quá trình phân tích một vài trong số chúng về nơi ông muốn đầu tư. Danh sách bao gồm các công ty blue-chip lớn ở Mỹ. Dưới đây là các cổ phiếu hoặc chứng khoán được đưa vào danh sách lựa chọn cùng với giá thị trường chứng khoán mới nhất của chúng, được biểu thị bằng đô la Mỹ, nơi anh ta đang cân nhắc đầu tư vào.
Bạn được yêu cầu tính toán Phạm vi và đưa ra biến thể mà danh sách có.
Giải pháp:
Dưới đây là dữ liệu được cung cấp để tính toán phạm vi.
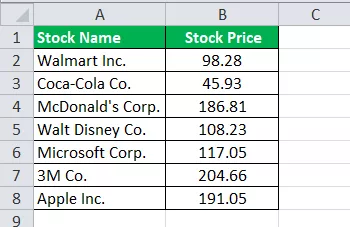
Sử dụng thông tin trên, việc tính Giá trị Tối đa trong excel sẽ như sau,

Giá trị tối đa = 204,66
Cách tính Giá trị Tối thiểu trong excel như sau,
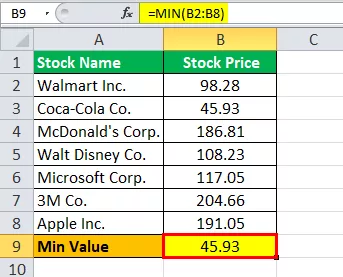
Giá trị tối thiểu = 45,93
Do đó, việc tính toán phạm vi như sau,

Phạm vi = 204,66 - 45,93
Phạm vi sẽ là -
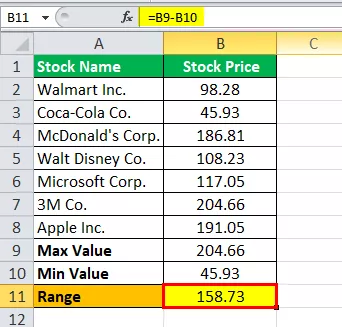
Phạm vi = 158,73
Sử dụng công thức phạm vi
Phạm vi, theo cách riêng của nó, rất dễ dàng và rất cơ bản để hiểu cách các số trong tập dữ liệu đã cho hoặc mẫu đã cho được trải ra bởi vì, như đã nêu trước đó, nó tương đối dễ dàng để thực hiện phép tính vì có chỉ yêu cầu của một phép toán số học rất cơ bản chỉ trừ giá trị tối thiểu cho giá trị lớn nhất, nhưng phạm vi nó có ít ứng dụng hơn cho một tập dữ liệu nhất định hoặc một mẫu nhất định trong thống kê. Phạm vi cũng hữu ích trong việc ước tính một thước đo chênh lệch khác, được gọi là phương sai hoặc độ lệch chuẩn.
Phạm vi, như đã đề cập trước đó, chỉ có thể thông báo về các chi tiết cơ bản, tức là, mức độ lan truyền của một mẫu nhất định hoặc tập hợp dữ liệu nhất định sẽ nằm ở đâu. Bằng cách đưa ra sự khác biệt hoặc nói phương sai giữa các giá trị cao nhất và thấp nhất của một mẫu nhất định hoặc tập dữ liệu đã cho, nó cung cấp một thông tin hoặc một ý tưởng sơ bộ về các quan sát cực đoan quan trọng về mức độ lan truyền rộng rãi của các quan sát đó, nhưng một lần nữa nó không cho gợi ý hoặc bất kỳ thông tin nào về các điểm dữ liệu khác mà chúng sẽ nằm ở đâu, đó là điểm yếu chính của việc sử dụng phương trình phạm vi.
Phạm vi, như đã thảo luận ở trên, hữu ích để mô tả mức chênh lệch trong một mẫu nhất định hoặc một tập dữ liệu nhất định và hơn thế nữa cũng được sử dụng để so sánh mức chênh lệch kết quả giữa cùng một mẫu đã cho hoặc cùng một tập dữ liệu nhất định.








