Máy tính tiết kiệm đơn giản
Máy tính Tiết kiệm Đơn giản có thể được sử dụng để tính toán số tiền đáo hạn sẽ có sẵn cho cá nhân trong đó anh ta có các tùy chọn để đầu tư và anh ta sẽ chọn trong đó anh ta có thể tối đa hóa lợi nhuận của mình.
Máy tính tiết kiệm đơn giản
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1) / r
Trong đó,- Tôi là số tiền đầu tư ban đầu.
- r là lãi suất.
- n là số kỳ tiết kiệm đơn giản sẽ được thực hiện.
- F là tần suất trả lãi
- i là số tiền cố định được đầu tư đều đặn.
Giới thiệu về Máy tính Tiết kiệm Đơn giản
Công thức như sau:
Về mặt toán học, nó có thể được tính cho Tiết kiệm Đơn giản một lần:
M = I * (1 + r / F) n * FThứ hai, nếu tiết kiệm đơn giản hàng tháng, cách tính:
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1 / r)Trong đó,
- M là tổng số tiền cuối kỳ tiết kiệm giản đơn
- Tôi là số tiền đầu tư ban đầu
- tôi là số tiền cố định được đầu tư đều đặn
- r là lãi suất
- F là tần suất trả lãi
- n là số kỳ tiết kiệm đơn giản sẽ được thực hiện.
Có rất nhiều ngân hàng và các tổ chức tài chính khác đang cạnh tranh trên thị trường để thu hút tiền gửi để họ có thể kinh doanh nhiều hơn, tức là cho các doanh nghiệp hoặc cá nhân có giá trị ròng cao cho vay. Một số ngân hàng sẽ trả lãi suất cao hơn nếu số tiền gửi vượt quá giới hạn ngưỡng nhất định và được duy trì trong tài khoản, hoặc nếu không, họ sẽ trả lãi suất tiêu chuẩn. Hơn nữa, có thể có sự khác biệt về tần suất trả lãi; ví dụ, tiền lãi có thể được gộp và trả hàng quý, nửa năm hoặc hàng năm tùy thuộc vào ngân hàng. Do đó, với máy tính này, các cá nhân sẽ có thể xác định tổ chức tài chính nào họ nên chọn để đầu tư tiền của mình bằng cách so sánh số tiền đáo hạn hoặc lợi nhuận kiếm được trên số tiền gốc của họ.
Làm thế nào để tính toán tiết kiệm đơn giản?
Người ta cần làm theo các bước dưới đây để tính toán khoản tiết kiệm đơn giản.
Bước # 1 - Xác định số tiền sẽ được đầu tư, cho dù đó là khoản đầu tư gộp hay cũng là khoản đầu tư định kỳ, sau đó cần xem xét điều tương tự khi tính toán tỷ lệ tiết kiệm.
Bước # 2 - Tìm ra tỷ lệ lãi suất có sẵn trong các lựa chọn cho cá nhân, và lãi suất đó sẽ kiếm được hoặc dự kiến sẽ kiếm được từ khoản tiết kiệm đơn giản.
Bước # 3 - Bây giờ, hãy xác định khoảng thời gian mà nó sẽ được đầu tư, và chủ yếu là những khoảng thời gian đó sẽ là dài hạn và sẽ tùy thuộc vào từng trường hợp.
Bước # 4 - Chia lãi suất cho số kỳ tính lãi hoặc lãi suất Tiết kiệm đơn giản được trả. Ví dụ, nếu lãi suất được trả là 5% và nó trả hàng tháng, thì lãi suất sẽ là 5% / 12, tức là 0,416%.
Bước # 5- Bây giờ, hãy sử dụng công thức đã được thảo luận ở trên ở điểm 1) trong trường hợp Tiết kiệm Đơn giản được tạo thành gộp và sử dụng công thức 2) trong trường hợp Số tiền Tiết kiệm Đơn giản được thực hiện đều đặn cùng với bất kỳ số tiền ban đầu nào cho tất cả các tùy chọn có sẵn .
Bước # 6 - Con số kết quả sẽ là số tiền đáo hạn sẽ bao gồm cả thu nhập Tiết kiệm Đơn giản và chọn một trong những khoản thanh toán cao nhất về lãi suất.
Ví dụ về Máy tính Tiết kiệm Đơn giản
Anh William hiện đã trưởng thành và rất hào hứng khi mở tài khoản tiết kiệm đầu tiên của mình. Anh ấy đã tìm kiếm tổ chức tài chính, nơi cung cấp lãi suất cao, nhưng anh ấy bối rối vì không biết ngân hàng nào sẽ cung cấp cho anh ấy lợi tức cao nhất. Dưới đây là những trích dẫn mà ông William đã lọt vào danh sách.

Anh ta muốn đầu tư 1.500 đô la vào một trong hai tài khoản và anh ta sẽ đầu tư theo cách mà tài khoản đang trả lãi. Ví dụ, nếu ngân hàng thanh toán nửa năm một lần, thì số tiền sẽ được đầu tư như nhau vào cuối mỗi kỳ và sẽ tiếp tục như vậy trong thời gian 10 năm.
Dựa trên thông tin đã cho, bạn được yêu cầu tính toán số tiền mà anh ta sẽ tiết kiệm, lãi suất thu được từ cùng một khoản, và anh ta nên chọn đầu tư vào Ngân hàng nào.
Giải pháp:
Chúng tôi được cung cấp các chi tiết dưới đây:
NGÂN HÀNG TÔI
- I = Số tiền ban đầu sẽ bằng 0
- r = Lãi suất là 3,00% và Hàng quý sẽ là 3,00% / 4 là 0,75%
- N = Tần suất hàng quý ở đây; do đó nó sẽ là 4
- n = số năm Tiết kiệm Đơn giản được thực hiện, ở đây là 10 năm.
- i = Đây là số tiền thường xuyên được đầu tư, là 1500/4 tức là $ 375

Bây giờ, chúng ta có thể sử dụng công thức dưới đây để tính số tiền đáo hạn.
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1) / r
- = 0 * (1 + 0,75%) 10 * 4 + 375 * ((1 + 0,75%) 10 * 4 - 1 / 0,75%)
- = 17.417,43
Số tiền đáo hạn sẽ là 17.417,43
Lãi gộp kiếm được sẽ là $ 17.417,43 - $ (375 * 40) = $ 2,417,43.

NGÂN HÀNG II
- I = Số tiền ban đầu sẽ bằng 0
- r = Lãi suất là 3,12% và Nửa năm sẽ là 3,12% / 2 là 1,56%.
- N = Tần suất là Nửa năm ở đây, do đó nó sẽ là 2
- n = số năm Tiết kiệm Đơn giản được thực hiện, ở đây là 10 năm.
- i = Đây là số tiền thường xuyên được đầu tư, là 1500/2 tức là 750 đô la

Bây giờ, chúng ta có thể sử dụng công thức dưới đây để tính số tiền đáo hạn.
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1 / r)
- = 0 * (1 + 1,56%) 10 * 2 + 750 * ((1 + 1,56%) 10 * 2 - 1) / 1,56%
- = $ 17.445,58
Giá trị đáo hạn sẽ là $ 17.445,58
Lãi kép kiếm được sẽ là $ 17.445,58 - ($ 750 * 20) = $ 2,445,58.

NGÂN HÀNG III
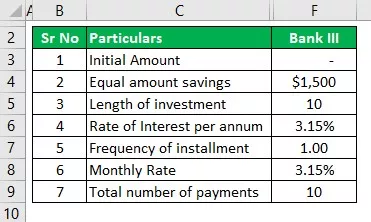
- I = Số tiền ban đầu sẽ bằng 0
- r = Lãi suất, là 3,15% và Hàng năm sẽ là 3,15% / 1, là 3,15%
- N = Tần suất ở đây là Hàng năm, do đó nó sẽ là 1
- n = số năm Tiết kiệm Đơn giản được thực hiện, ở đây là 10 năm.
- i = Đây là số tiền thường xuyên được đầu tư, 1500/1 tức là 1.500 đô la
Bây giờ, chúng ta có thể sử dụng công thức dưới đây để tính số tiền đáo hạn.
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1) / r
- = 0 * (1 + 3,15%) 10 * 1 + 1500 * ((1 + 3,15%) 10 * 1 - 1) / 3,15%
- = $ 17.315,08
Số tiền đáo hạn sẽ là $ 17.315,08
Lãi kép kiếm được sẽ là $ 17.315,08 - ($ 1500 * 10) = $ 2.315,08.

Số tiền cao nhất kiếm được là ở Ngân hàng II, và do đó anh ta nên mở tài khoản ở Ngân hàng II.

Phần kết luận
Máy tính này, như đã thảo luận ở trên, có thể được sử dụng để so sánh các số tiền đáo hạn khác nhau giữa các tổ chức tài chính vì tỷ lệ lãi suất cao hơn không đảm bảo số tiền tuyệt đối cao nhất, như đã thấy trong ví dụ trên. Do đó, người ta nên tính toán và so sánh số tiền trong kỳ hạn thanh toán và sau đó đưa ra quyết định.